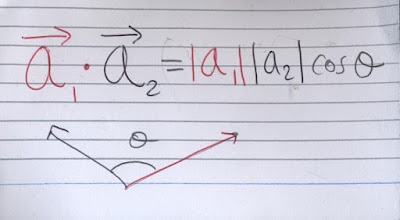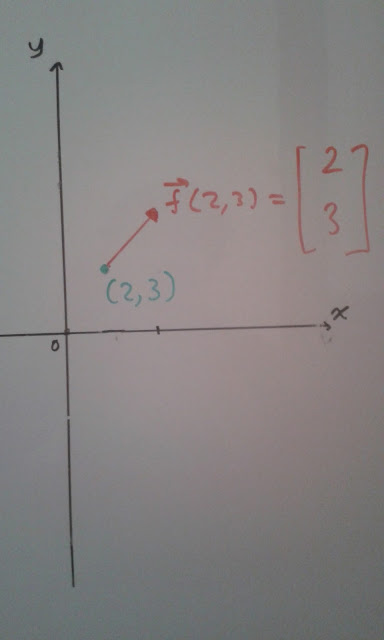The Dot and Cross Product

 

             Before we begin, let me make some clarifications. A vector is represented by a letter which is often written as bold in text to distinguish it from scalars. When representing a vector with an arrow, the tail is defined to be the starting point of the vector, and the tip is defined to be the end point of the vector

            Vectors are often defined as having separate, independent components. We showed that in two dimensions, every vector that exists can be described uniquely as a sum of the product of the basis vectors, which is the formal name for the unit vectors i-hat and j-hat, and uniquely determined constants c1,c2. This also is the case for three dimensional space, but three independent constant are required, c1,c2 and c3. The visual interpretation that follows is that every vector in three dimensional space therefore can be 'broken' down into vector components which are parallel to the x, y, and z axis.

           .

Component by component: the physical meaning

           This is a very useful concept in physics, as it allows us to independently consider what a particle which is acted on by a force experiences in the x,y and z direction. Then, we can take the vector sum and see what the net force on the object is, and use F=ma to figure out its net acceleration.

          Another use in breaking forces down into component is to figure out the work done on an object. Suppose a particle is attached to a horizontal rail, which can be represented as the x-axis. After being acted on by a steady, constant force which makes a positive acute angle ϴ the horizontal, the particle accelerates and gets displaced by a certain amount. Force and displacement are both represented by vectors, so if we place the particle at the origin of our 2-D coordinate system, the force vector F and the displacement vector s (vectors are written in bold in text) will have their tail both rooted in the origin.

          Now, if we break the force into components, there will be a vertical component of F pointing up and a horizontal component of F pointing to the right. Now, since there are other forces acting on the object, i.e its weight and the traction due to the rail, (but we assume no friction) we assume that all the vertical components cancel out and the only net force on the object is the horizontal component of F.  Only the horizontal component of F does work on the object. Since Work=Force times distance, the way we calculate this is to simply take the magnitude of the horizontal component of F, which is by simple trig Fcos(ϴ) and the magnitude of the displacement vector s.

The Dot Product

       This is such common practice that we give this process a name: it is called taking the dot product of two vectors.

 In general, the dot product of v and w is defined as the product of their magnitudes and the cosine of the angle in between. Note that the dot product takes in two vectors and outputs a regular number, a scalar. Since the magnitudes of v and w and cos ϴ are all numbers, we are free to change the order as we please. This implies an important property of the dot product: commutativity.

     

           There are more important properties which is implied by the definition; the dot product is distributive; since the definition only involves the product of three scalars, it follows that the order shouldn't matter. Another important one comes from the trigonometric function involved: the dot product of two orthogonal (fancy word for perpendicular) vectors is always zero. A third property is that the dot product of a vector with itself is its magnitude squared, since the angle in between is 0.

           Here is a less obvious property. In taking the dot product of v and w, suppose that I throw in a scalar in there. In other words, suppose that the vector v, let's say, can be written as a scaled version of a third vector, u. v=cu.
Using the definition, we end up with the dot product of v and w being |v||cu|cos (theta).
The cosine theta is no problem, but how do we deal with the second term, |cu|?
Well, using similar triangles, we can argue the following. Since the x and y component of u is multiplied by c to give the vector cu, the hypotenuse of a right triangle created by breaking u into its x and y components must also have its length scaled by c. But the length of the hypotenuse really is geometrically equivalent to the norm or magnitude of u, so the magnitude of cu must be c times the magnitude of u, or in other words, |cu|=c|u|.
           Some more important properties involve the zero vector: a vector whose every component is zero. Following from the fact that the zero vector has zero magnitude, the dot product of a vector with the zero vector is always the number zero.

Below is a handwritten summary of a good number of dot product properties we have used, the list from which I took from the website <chortle.ccsu.edu/vectorlessons/vch07/vch07_8.html>.

An interesting duality: makes life alot easier!

    I hope you agree with me in saying that this definition is pretty intuitive, and it fairly rigorous as well- except for the ambiguity of which angle we use (it doesn't really matter, but the angle less than pi radians is often chosen). However, it is a real pain to compute. It isn't even defined in three dimensions, let alone n dimensions! Furthermore, one has to compute the magnitude of the vector, and the direction! It is totally defined for more than two vectors, but it can end up being a real headache!
   It turns out that this really neat duality exists between this physical representation of the dot product and a mathematical object that you have met before- matrices. Now, matrix multiplication isn't even defined technically for  n by one with n by one vectors, but the process you take the dot product is very similar.

Therefore, to compute the dot product of two or more vectors, simply take the sum of the product of the corresponding components!

Another proof does exist for the dot product using the law of cosines, but I would at this point challenge the reader to derive this alternate proof.


CROSS PRODUCT

    In elementary physics, we like to assign vectors associated to rotation. For example, the torque of an object is defined as the perpendicular component of force multiplied by distance from pivot point. Actually, this is incomplete, since we want to define torque as a vector. Why? To remove ambiguity. I could apply the same resultant force to the right of the pivot with the same angle, and in a different scenario, the same force to the left of the pivot with the same angle but get an opposite effect. Therefore, we define the torque vector in the latter case to point in the opposite direction as in the former case, albeit having the same magnitude.
   We can imagine defining a vector r which represent the point at which we apply the force: starting at the pivot and ending at that mentioned point. Force F is already a vector. Because it is the vertical component that we care about, it will be the magnitude of the force times the magnitude of the displacement from pivot times the sine of the angle in between.
 To complete this, we want to add direction. The cleanest way to do this is to define a unit vector which is orthogonal to both vectors in the plane, hence requiring the z axis. The direction is defined by the right hand rule: if the quickest way to get from the first vector to the second vector is to walk anti-clockwise, the normal unit vector will pop out of the page and towards you. If it is clockwise, then the normal unit vector will pop into the page and away from you.
Finally, putting it all together, we multiply the magnitude of the torque, given by |F||r|sin theta with the normal unit vector, so that we get a vector which points in the desired direction with desired magnitude.

Using this definition, we can immediately infer a property of the cross product of u and v, namely that it is anticommutative, or in other words, u×v =  -(v×u).

I would say that this is fairly intuitive actually, because if F and r were to switch places, like in the example above, the direction you would have to walk from the first to the second vector would be opposite, and so the direction of the cross product vector would be also opposite. Since theta is the same, and since the magnitudes are unaffected, the magnitude would be the same for both vectors, but the minus sign simply reflects the fact that the two cross product vectors point in the opposite direction.

Just like in the dot product however, if I were to take the cross product of a vector cu, where c is a scalar, then: : (cu)×v=|cu||v|sinϴ=c|u||v|sin=c(u×v)
We can also deduce other properties of the cross product, for example it is distributive over a sum:
(u+v)×w=|u+v||w|sinϴ n=(|u||w|sinϴ +|v||w|sinϴ)n= (|u||w|sinϴn +|v||w|sinϴn)=u×w+v×w
which is seen before in the dot product.

Note that although it requiring three dimensions, this cross product definition doesn't give us a direct way to compute the cross product of three dimensional vectors. Let's derive it now, using the definition and basic properties.

First of all, we need to discuss how the three dimensional cartiesan coordinate system is orientated. The question is, there is a convention of which way the positive y axis and the positive x axis is orientated, but for the positive z axis, which way will it be orientated? Unsurprisingly, the z-axis is defined by the right hand rule; point your index finger in the direction of the increasing x axis, your middle finger in the direction of the increasing y axis, and your thumb will point in the direction of increasing z axis. Let's rephrase this definition of the cross product: the x unit vector i-hat cross y unit vector j-hat must be the z unit vector k-hat.

Let's now elaborate and find more rules. We can milk j i -k using anticommutativity. Here are a list of equations linking the basis vectors using the cross product:

Now we are ready to find a general formula that gives us a cross b in terms of the components of each vector. 

Expanding out, and simplifying using the cross products of the unit vectors discussed earlier, we arrive at the final formula.

Now, it turns out that this expression is exactly the same as taking the determinant of a three by three matrix with the components of the a and b unit vector, and the i,j and k-hat unit vectors all arranged in a praticular manner.

If you are unfamiliar of taking the determinant of a three by three matrix, or what a matrix even is, I will for now provide you with a superficial explanation. A matrix is simply an array of numbers, arranged into rows and columns. It is, if you like, a table of quantities. A matrix can have as many rows or column as one likes, and it does not even have to be finite!
For special types of matrices, called square matrices, which have the same number of rows and columns, there is a single number which is quite useful to know, called a determinant.
To find a determinant of a 2 by 2 matrix, take the difference of the product of "northwest-southeast" diagonal number and the product of the "northeast-southwest" diagonal.
Finding a determinant of a higher dimension matrix is somewhat of an iterative process. The process for a 3 by 3 matrix is described below:
 

And then, if you list the unit vectors on the top row, and then the components of the first vector in the second row, and the components of the second vector in the third row in a 3 by 3 matrix, the determinant turns out to be simply a cross b.

Update on EPQ research

           Primarily, I have dedicated to this blog to my main passion of communicating ideas in mathematics to readers, and also venturing into the technical details. In this blog post, I aim to do something slightly different: I would like to explain what my actual EPQ is, and what stage I currently happen to be in.

           My EPQ is based on Maxwell's equations, and I have been doing some background research for the past month. I believe I underestimated the depth that I end up going into the mathematics behind it, and currently haven't explored the physics application of all of this research. Furthermore, I have found myself working behind schedule, even though I have been keeping at this consistently every day. I have yet to refine my topic idea in Maxwell's equations; it is still a work in progress, despite it being into mid August.
          I aim to keep it simple, and discuss in my ultimate dissertation what the importance of maxwell's equations were, and why it is a corner stone in physics. It is the first successful attempt at unifying electricity and magnetism, and the fundamental postulate in physics, that there are quantities which remain invariant under what are called Lorentz Transformations was first implied by this. Namely, the speed of light as a universal constant, which is the heart and veins of relativity, fell straight out of these equations.
        I believe I owe a quick explanation to the reader what a Lorentz Transformation is. Simply put, it is the mathematical process of switching between two non-accelerating, called inertial, reference frames, which move with a relative constant velocity to each other. As an example, if I compared what flow of time and what measurements of distance an observer moving in a space ship at half the speed of light (with no acceleration) as opposed to an observer on earth would experience, I would have to perform a Lorentz Transformation. At either case, the guiding principal behind the mathematics is the fact that some quantities are the same universally, i.e. do not vary, or in other words, remain invariant, such as the speed of light and the path between spacetime, under these Lorentz transformations. I shall end this here, lest I digress into relativity.
         
            My plan from this point on is to pick up more speed in my research. I have a five day vacation planned soon, and then the year thirteen begins with all the UCAS application process, so I really should aim to be done completely in terms of background research by then.

         In terms of my background research, I have used the following resources: Khan Academy, Yale lectures by Dr. Ravi Shanker, My Young Freedman University Physics textbook and finally a Vector Calculus book by Springer Undergraduate Mathematics Series, written by R.C Matthews.

        Let me delve into the concepts which I covered and feel fairly confident in: Understanding multi variable functions, differentiation in multivariable calculus (the partial derivative, the gradient, the directional derivative, curl, divergence, the vector valued function and the formal definition, multivariable chain rule), topics borrowed from linear algebra (span, vectors, cross and dot product, proof of these formulae), integration in multivariable calculus (double, triple integral, surface integrals, line integrals, conservative vector fields, intuition, derivation and intuition of the fundamental theorem of line integrals (which is a cousin to the fundamental theorem(s) of calculus), and flux in 2D) In physics, I have studied mainly from the Yale lectures and the uni physics textbook on the following topics, electrostatics, electric fields, symmetry arguments, and Gauss' law, which is the first of maxwell's equations. Got plenty of more content to cover, however.

Basic intro to vectors, addition and multiplication by a scalar.

Thinking about vectors

          Vectors, for the purposes of elementary physics, is a quantity which has two separate pieces of information embedded in it: magnitude (sometimes called the norm) and direction. At least this is the interpretation which we will use. Vectors are often depicted as arrows, where the arrow's length typically corresponds with the magnitude, and its orientation corresponds with direction. Vectors can be depicted in one, two, or three dimensions, and can even live in n dimensions greater than three, but then it becomes impossible to visualise as a simple arrow in space. For the purposes of using vectors for physical phenomena such as electromagnetism, we shall constrain ourselves to no more than three dimensional space. 

How is magnitude and direction defined?

          To describe a vector fully the direction and magnitude has to be specified. There are many ways of doing this, and they are all correct so long as there is absolutely no ambiguity over what the magnitude and direction of the vector being described. The methods of describing it will be described later on in this article.

A Useful property of vectors

        

          Due to the way that we have defined a vector as being a quantity of only magnitude and direction, a useful property is implied when we imagine vectors as arrows in space. 

      I like to think of a vector as a set of instructions for movement: "Walk x metres in this direction." Then, imagine asking it, "Ok, where do I start from?" Then the vector will reply: "I don't care."

          The vector only gives information about the direction and magnitude of movement. Hence, it doesn't matter where the initial point is, and by that logic that implies that  two vectors which have the same magnitude and direction but placed at the point (2,2) and the other placed at (-1000,23.4533234) are equivalent. 

          Since it doesn't matter where you root your vector, in mathematics we tend to place the tail at the origin because it makes calculations simple.

Two elementary operations on vectors

        There are two fundamental operations which one can perform on a vector. It is vector addition, and scalar multiplication. There are more of course, but these two are the springboard. 

  Vector addition

          Suppose that we take a really simple space where we can perform our vector operations in, the one-dimensional number line. And suppose, vector v tells you to move 6 meters to the right, and vector w tells you to move 3 meters to the left. Now, imagine that we were interested in the combined effect of v and w. What does doing v first and then doing w second effectively amount to? In other words, what does v+w look like?

        We can display v and w as two separate arrows. Here they are:

vector v

vector w

        Now, try to imagine a graphical way to represent this combined effect that v and w has. 

Hint: use the previously discussed fact that you can slide any of the two vectors along anywhere that you desire along the number line without changing its identity.

        It turns out that if we take w and place the tail of the arrow onto the tip of v, then the tip of w lies exactly on top of the answer. Then, we can even further extend this idea, and define a new vector v+w to start at the point where we started, and end at the point where we ended. This new vector tells you straight away where you will end up without having to do v and w seperately.

"Adding" the vectors

v+w

 

      Now, importantly, this is the geometric equivalent of saying 3=(5)+(-2). And, just like how we can equivalently say that 3=(-2)+(5), it is the case that v+w=w+v.

     This can also be done in two dimensions and three dimensions. As a general rule, to find v+w, bring the tail of w so it touches the tip of v, and drawing an arrow from the tail of v to the tip of the newly placed w gives you the vector v+w. This can be done in the opposite order too.

Vector v and w rooted at the origin

Sliding or "translating" one of the vectors is allowed

The vector v+w starts at what I like to call the "free ends": the tail of the vector that wasn't moved, and the tip of the vector
that was moved.

Scalar multiplication

           We used the idea of addition from arithmetic to explain vector addition, and show that they are fundamentally the same idea. What about multiplication? 

           Well, suppose that we take vector v which tells you how far you have walked along the number line. Then, what would the vector 2v look like? That is easy. If you walked twice as far, the arrow representing the vector will be twice as long. In general, the magnitude of the vector cv is simply c times the magnitude of v. 

The Cartesian Starter Pack: Basis Vectors.

          Now, returning to the xy plane, there really are two vectors that you will ever need. A vector, which I will from now on use interchangeably with "arrow" which points horizontally and is of magnitude one, and another vector which points vertically and is of magnitude one as well.

We give these vectors names: i-hat for the former (which I will denote as simply i, don't confuse it with i from complex numbers), and j-hat for the latter (which I will also denote as j). 

        

 Take the i-hat unit vector, and scale it to the vector xi. Next, take the j-hat unit vector, and scale it to yj. 

I used x0 and y0 instead of just saying x and y to emphasise that these are arbitrary but particular points on the plane. There is no effective difference though, that is my choice of notation.

        Then, if you bring the tail of the vector yj to the tip of xi, it will touch the point (x,y). But this is vector addition, so this means that the vector v really is the same thing as saying xi+yj. 

That helpfully breaks our vector up into horizontal and vertical components, which is a very common practice in physics and mathematics- practice doing this!

           Hence, a vector which is rooted at the origin and represents a point (x,y) is given by v=xi+yj.

This vector describes a unique position on the x,y plane, so we give it a special name: the position vector, which you met in my previous blog.

           This can be extended to three dimensions, where the basis vectors are i,j, and k for the x,y, and z axis respectively.

Column vector notation

          Another popular way of denoting a vector v=xi+yj is also by writing the x and y components in a column vector form, shown blow.

V can be therefore written in terms of the i and j hat unit vectors, or in column vector notation.  A vector which is
rooted in the origin is often called a position vector, and the letter used instead of v often is r. 

Algebraic and Analytical vector addition and vector-scalar multiplication

  Let's now try to add two vectors v and w with x components x1 and x2 respectively, and y components y1 and y2 respectively. From combining like terms, we can algebraically prove that the sum of two vectors is the same as the sum of the corresponding components:

Similarly, we can also show that  the product of a vector and a scalar c is equivalent to the product of the x-component and c, the y-component and c, and so on:

           In column vector notation form:

 

 

Using Khan Academy to master multivariable calculus

 Survey of the Fundamental Concepts in Multivariable Calculus.

    As I build the foundational work for my EPQ research, I have extensively used the amazing educational website khan academy to master fundamental mathematical tools and concepts defined in multivariable calculus. At the time of the last edit, the 6th of August, I have finished the sub-courses on visualising multivariable functions, differentiating multivariable functions, and now I am studying integrating multivariable functions. I have taught myself the essence of line integrals, and now I am studying two dimensional flux.

Let the Maths Begin!: Revisiting Functions, Vectors, and Parametrisation

Scalar vs. Vector Valued Functions

    To begin, I would like to introduce another type of function that you may not be used to yet: the vector-valued function.

     A scalar valued function is essentially what is meant in everyday maths life when one says: "function." It is something that takes in a scalar and outputs a scalar.
    To get a more concrete idea of what a scalar function is, and to revisit the underlying intuition, it is useful to think of a scalar valued function like this: feed it a point on a number line (for a single-variable scalar function,) or on the xy plane (for a two variable scalar function) or in space (for a three-variable scalar function) or in n dimensions, and it will return another single scalar value: a number.
    In other words, there could be n dimensions in the input space, with n different variables, such as x,y,z, etc. but only one scalar value is returned in any case. What we often consider in single variable calculus is an input space being a number line (hence it being a one-dimensional input space) and the output being a number line, too. In this case, the dimensions of what goes in matches the dimensions of what goes out.

  (Note: in my diagrams, I will often denote green as the input space and red as the output space for the ease of the reader).

Figure 1

Two times two equals four: This is the typical visualisation of functions actively mapping numbers from set A to set B.
Instead of numbers just existing as a list in A and B, it is more convinient to depict the numbers sitting on a number line, since the domain and range here are continuous. Here, I have chosen the function f(x)=2x as an example, and a point x=2 gets mapped to f(2)=4.

Figure 2

This is a more common way to visualise functions: I have made the x and f(x) number lines perpendicular
to one another, in effect merging the input and the output space into a two dimesnional plane. I chose the x to be on the horizontal axis by convention. Here, I visualise this line, the graph of f(x)=2x as 'guiding' the input point 2 to the point 4 on the f(x) axis.
A less complicated way of visualising this is to define the vertical axis as the y axis, another variable separate to x.
The points (x,y) that satisfy the equation y=f(x) form a line, or a curve, which is called the graph of the function. 

    To make what we mean as a multivariable scalar function more concrete, here the same idea, extended to a two dimensional space onto an output number line. Take note that regardless how many dimensions I choose my input to be, the output will always be a one-dimensional input. Here is a visualisation:

    The common and convinient way here is to merge the input and output space yet again, and so we have two dimensions from the input and one dimension from the output, giving us a graph which requires three dimensions, an x and y axis and a z axis which is a function of x and y. The resulting graph will be a two dimensional surface, like the one depicted below. Note that I have put the graph in a box, but that has nothing to do with the actual function. It just nicely frames the graph. 

Observe below how the same point we probed last time, (π/6,π,3) gets mapped to the point z=13/4. 

Consequently, when we merge the two spaces together, (π/6,π/3,13/4) lies directly above

(π/6,π/3,0).

The z value corresponds to the height of the graph, just like in single variable function.

Vector Valued Functions

    I would now like to introduce the idea of a vector valued function. It is quite a simple idea: the function inputs a scalar (or a vector) but outputs strictly a vector. The first instance when one is introduced to this idea is when two mathematical tools are combined: parametric equations and the position vector.

Parametric Equations

      Parametrisation in the xy plane occurs when a parameter, a fancy word for a variable that does not have its own axis (unlike x and y), which is typically denoted by the letter t, is used to define points that lie on a path along the cartesian plane. The path defined by the curve is made up of all points (x,y) such that x and y are independent functions of t. An example of a use of this construct in physics is that if we observe that a particle travelling in two dimensions whose x and y coordinates can be defined as a function of time separately, then using parametrisation we can graph its journey given a time frame that we choose.
    Since each point that lies on the line is a function of t, it is given by the coordinates ( x(t), y(t) ). Then, x and y are defined separately. For example, x(t)=rcos(t) and y(t)=rsin(t) trace out a circle of radius r. Very importantly, however, we tend to restrict the domain of t; there are several reasons for this. First, we tend to want to end up with a curve which is finite, that has a definite start and end point. Secondly, t usually represents time, and the curve "driven" by the t on the xy plane is defined from t=0 onward. In the example of the circle above, the domain on t is 0 ≤ t ≤ 2π. Of course, the domain is arbitrary. If we wanted to trace out a semicircle, then 0 ≤ t ≤ π is the appropriate domain. Note: we only work in radians in 'higher' mathematics, and I will never switch to degrees unless I state otherwise.
 Since I glossed over the details here, I will aim to write a separate article on parametric equations, since it is very important indeed.

Position Vectors

    Now, as we progress in our study, we take a nuanced approach at parametric curves. First, I must explain that every point in space can be represented by a vector. This is the case for any n-dimensions of spa choose. For example, in one dimension, a point on the number line can be represented by a vector whose start point, its tail, sits at zero and whose end point, or tip, lies on the given point on the number line. The vector will have a length and a direction, the length being the distance travelled along the vector, and the direction in this case being left or right.

In two dimensions, a point (x,y) would be represented by a vector whose tail lies on the origin (0,0) and whose tip extends to the point (x,y). Note: x,y can be any point, even (0,0) itself, in which case the vector would have zero length.

    This special vector is called the "position vector." The two separate pieces of information we need in order to deduce the point which the vector is trying to represent is the length and direction. Length is also referred to as the magnitude of a vector, and in higher mathematics, the magnitude of a vector is called its "norm", and in particular, its "Euclidean Norm".  I will henceforth call the length of a vector its norm. The common notation for this is to put two bars around the vector: ||v||.

    In one dimension, the norm of a vector is identical to taking the modulus of the difference of the end value of x and the start value of x. In other words, if you want to find the norm of the vector in one dimensions, simply put the start point on zero, and take the modulus of the end point x. This is the actual value of the vector. In the case above, v=-2. The norm, or length of v is identical to the modulus to the vector, and the direction can be deduced by looking at its sign.

    In two dimensions, finding the norm is less intuitive: it is calculated by taking the positive square root of the sum of the squares of the x and y component of the vector, by the pythagorean theorem, and in three dimensions, the square root of the sum of the squares of the x, y and z components, and so on into n dimensions. In two dimensions, we give the direction of the vector by the angle it makes with the positive x-axis. In three dimensions, we need three separate angles, the angles it makes with each axis, and this carries on to n dimensions.

Now, there is one last thing I want to note: because the two key pieces of information embedded in the blue print of the vectors is length and direction, the starting points and end points do not matter. Hence, you can argue that the vector representing the point (2,3) could start arbitrarily any where. However, to make life easier, we tend to attach the tail of the position vectors to the origin, so the tip touches the point that we are interested in. Therefore, all points in our n-dimensional space can be uniquely represented by one and only one vector.
   As a quick review, there are two very important operations that can be done to vectors which I will assume that you are confident in. There is addition of vectors, which is visually found through the tip-to tail procedure, and the scalar multiplication of vectors: multiplying a vector by a number, called a "scalar," never affects its direction, but will multiply the norm by the scalar. Finally, we define a vector which is of length one along the x axis the i-hat unit vector, and a vector which is also of length one but point up the y-axis the j-hat unit vector. These vectors follow all the rules of addition and scalar multiplication just like any other vector.

    Let me illustrate first how to define a position vector for the point (2,3) on the xy plane. Consider two separate vectors, on which is pointing to the right and has 2 units of length, and the other pointing up and has 3 units of length. The vector pointing along the horizontal can be represented by a unit length vector i-hat, but scaled up by 2. Similarly, the vector pointing along the y-axis can be represented by a j-hat unit vector, but scaled up by a factor of 3. Again, where we place these vectors is arbitrary, so I will place them such that it will lie tip to tail. Ah! But that is vector addition, so really the position vector for (2,3) is identical to saying the sum of the horizontal and vertical vectors. Therefore, the position vector for (2,3) is

You will notice that there is an exact correspondence here: the position vector for a given (x,y) is simply the the x-value, a scalar, multiplied by the i-unit vector, and the y-value multiplied by the j-unit vector.  Therefore, for a position vector centred at the origin, the point (x,y) on the plane is represented by a vector r=xi+yj.
    We already established that for a given value of t (that lies in its domain) the parametric equations will output a coordinate ( x(t), y(t) ). For example, the point along the path at t=0 will be given by ( x(0), y(0) ). Now, the point on the curve at t=0 will be a point on the xy plane, and as I have shown earlier, this can be represented by a position vector r=x(0)i+y(0)j.
By that reasoning, we can define a separate position vector for t=1, which will then be r=x(1)i+y(1)j and t=2, which would be, you guessed it, r=x(2)i+y(2)j, and so on and all the infinite values of t in between, and for all the values of t for which this parametric curve is defined for.

    Now, you can immediately point out that if you give me an arbitrary value for t, I will give you a position vector. Well, that is suspiciously similar to the idea of a function, but with the only difference that the input is a scalar, a value for t, and the output is a vector. And that, ladies and gentleman, is an example of a vector-valued function, namely, a position vector valued function.

To represent the point (x(t),y(t)), we can define a position vector whose tail lies on the origin, and whose x and y components are given by the above formula.

Visualisation of a position vector function for any t in the closed interval [t0,t1].

  Vector Fields

Defining a position vector valued function turns out to be extremely useful for future use. In addition to this position vector valued function, other vector valued functions can be defined. For example, one could define a vector valued function in the xy plane which is not necessarily parameterised, but depends on x and y. In other words, instead of it being you give me a t and I give you a vector, we could also define a vector such that you give me a point on the plane or in space, and I give you a vector. Note, the vector is two dimensional, too. This vector is often visualised as being attached to the particular input point. This ends up being very very important by creating an infinite amount of vectors for each point on the plane, or in space, or in n dimensions, and can describe, for example, the force a particle would feel at that point. Whenever we have the same number of dimensions in the input and output, we can visualise the vector-valued function as a vector "field."
 In this case, as illustrated below, a point from a 2-dimensional input space gets mapped to a vector in the output space. As an example, observe how the point (2,3) gets mapped to the vector 2i+3j, according to the way I have defined the function.

The point (2,3) gets mapped onto the vector 2i+3j. The vector, by convention, not by fundamental mathematical laws, is centred at the origin.

Now, since the vector does not care where I place it along the xy plane, I can bring it from the origin and make the start point coincide with the point that I originally inputted into my function: (2,3). In a sense, I am merging the input and outputs spaces together, just like what you do when you graph regular single-variable scalar functions or even 2-variable scalar functions.

In just the same way I am perfectly allowed to chose to place my vector in the origin, I can place it starting from any point I want. In this case, so we can see 

Here, one can clearly see that the input, the green point, and the output, the red vector has been merged together onto a single xy plane.

 In theory, I can perform this to all the points on the xy plane and its output vectors, but it will take me quite a bit of time considering that there are an infinite amount of them! Therefore, I choose to display a subset of all the vectors that do exist. I used the website https://kevinmehall.net to graph the vector field in full f(x,y)=xi+yj. 

Vector fields then are super useful in physics as they can represent physical quantities. If you imagine fluid particle flowing through space, a vector associated to each point can very succinctly describe the velocity that a particular particle passing through that point would feel. Or, we can construct a vector field that would describe the force a positive test charge would feel at a given point in space due to another positive charge sitting at the origin of our coordinate system.

    And now we are developing ideas that will be exceptionally relevant and useful in our discussion of electricity and magnetism, particularly maxwell's equations. However, we shall now venture into the "calculus" of multivariable calculus. That shall be the topic of the next blog post.

Preliminary Research: How and why I changed my topic

As of today, I have decided that my topic would be centered around Maxwell's equations. I aspire to delve into the physics and mathematics surrounding these elegant and breath-taking system of equations, and narrow my interest down to a question which I can spend my entire summer researching in depth.

Initially, I had decided on the topic of calculus of variations. My interest in this area of mathematics began when I stumbled upon Noether's theorem a year ago. Reading up on it, I realised that this function called the 'lagrangian' was used, and a recursive theme of using the principle of least action brought me to want to learn about this fundamental principle.
I had then soon after began watching an excellent YouTube series on this concept by a channel with the name of "physicshelps". After doing further research, I realised that the introduction was based on a lecture Richard Feynman gave in Caltech university.

However, I began to realise that calculus of variations is a rather difficult and inaccessible topic for me, and the resources are limited. Even someone who I know who did a pHD in mathematics admitted that he didn't need to use it that much. Despite being a very exotic topic, I decided to turn my attention to something that used more 'mainstrem' but similar mathematics, while being very elegant and important to physics: Maxwell's equations. This blog is dedicated to the content that I learn in order to understand and research Maxwell's equations.