Using Khan Academy to master multivariable calculus

 Survey of the Fundamental Concepts in Multivariable Calculus.

    As I build the foundational work for my EPQ research, I have extensively used the amazing educational website khan academy to master fundamental mathematical tools and concepts defined in multivariable calculus. At the time of the last edit, the 6th of August, I have finished the sub-courses on visualising multivariable functions, differentiating multivariable functions, and now I am studying integrating multivariable functions. I have taught myself the essence of line integrals, and now I am studying two dimensional flux.

Let the Maths Begin!: Revisiting Functions, Vectors, and Parametrisation

Scalar vs. Vector Valued Functions

    To begin, I would like to introduce another type of function that you may not be used to yet: the vector-valued function.

     A scalar valued function is essentially what is meant in everyday maths life when one says: "function." It is something that takes in a scalar and outputs a scalar.
    To get a more concrete idea of what a scalar function is, and to revisit the underlying intuition, it is useful to think of a scalar valued function like this: feed it a point on a number line (for a single-variable scalar function,) or on the xy plane (for a two variable scalar function) or in space (for a three-variable scalar function) or in n dimensions, and it will return another single scalar value: a number.
    In other words, there could be n dimensions in the input space, with n different variables, such as x,y,z, etc. but only one scalar value is returned in any case. What we often consider in single variable calculus is an input space being a number line (hence it being a one-dimensional input space) and the output being a number line, too. In this case, the dimensions of what goes in matches the dimensions of what goes out.

  (Note: in my diagrams, I will often denote green as the input space and red as the output space for the ease of the reader).

Figure 1

Two times two equals four: This is the typical visualisation of functions actively mapping numbers from set A to set B.
Instead of numbers just existing as a list in A and B, it is more convinient to depict the numbers sitting on a number line, since the domain and range here are continuous. Here, I have chosen the function f(x)=2x as an example, and a point x=2 gets mapped to f(2)=4.

Figure 2

This is a more common way to visualise functions: I have made the x and f(x) number lines perpendicular
to one another, in effect merging the input and the output space into a two dimesnional plane. I chose the x to be on the horizontal axis by convention. Here, I visualise this line, the graph of f(x)=2x as 'guiding' the input point 2 to the point 4 on the f(x) axis.
A less complicated way of visualising this is to define the vertical axis as the y axis, another variable separate to x.
The points (x,y) that satisfy the equation y=f(x) form a line, or a curve, which is called the graph of the function. 

    To make what we mean as a multivariable scalar function more concrete, here the same idea, extended to a two dimensional space onto an output number line. Take note that regardless how many dimensions I choose my input to be, the output will always be a one-dimensional input. Here is a visualisation:

    The common and convinient way here is to merge the input and output space yet again, and so we have two dimensions from the input and one dimension from the output, giving us a graph which requires three dimensions, an x and y axis and a z axis which is a function of x and y. The resulting graph will be a two dimensional surface, like the one depicted below. Note that I have put the graph in a box, but that has nothing to do with the actual function. It just nicely frames the graph. 

Observe below how the same point we probed last time, (π/6,π,3) gets mapped to the point z=13/4. 

Consequently, when we merge the two spaces together, (π/6,π/3,13/4) lies directly above

(π/6,π/3,0).

The z value corresponds to the height of the graph, just like in single variable function.

Vector Valued Functions

    I would now like to introduce the idea of a vector valued function. It is quite a simple idea: the function inputs a scalar (or a vector) but outputs strictly a vector. The first instance when one is introduced to this idea is when two mathematical tools are combined: parametric equations and the position vector.

Parametric Equations

      Parametrisation in the xy plane occurs when a parameter, a fancy word for a variable that does not have its own axis (unlike x and y), which is typically denoted by the letter t, is used to define points that lie on a path along the cartesian plane. The path defined by the curve is made up of all points (x,y) such that x and y are independent functions of t. An example of a use of this construct in physics is that if we observe that a particle travelling in two dimensions whose x and y coordinates can be defined as a function of time separately, then using parametrisation we can graph its journey given a time frame that we choose.
    Since each point that lies on the line is a function of t, it is given by the coordinates ( x(t), y(t) ). Then, x and y are defined separately. For example, x(t)=rcos(t) and y(t)=rsin(t) trace out a circle of radius r. Very importantly, however, we tend to restrict the domain of t; there are several reasons for this. First, we tend to want to end up with a curve which is finite, that has a definite start and end point. Secondly, t usually represents time, and the curve "driven" by the t on the xy plane is defined from t=0 onward. In the example of the circle above, the domain on t is 0 ≤ t ≤ 2π. Of course, the domain is arbitrary. If we wanted to trace out a semicircle, then 0 ≤ t ≤ π is the appropriate domain. Note: we only work in radians in 'higher' mathematics, and I will never switch to degrees unless I state otherwise.
 Since I glossed over the details here, I will aim to write a separate article on parametric equations, since it is very important indeed.

Position Vectors

    Now, as we progress in our study, we take a nuanced approach at parametric curves. First, I must explain that every point in space can be represented by a vector. This is the case for any n-dimensions of spa choose. For example, in one dimension, a point on the number line can be represented by a vector whose start point, its tail, sits at zero and whose end point, or tip, lies on the given point on the number line. The vector will have a length and a direction, the length being the distance travelled along the vector, and the direction in this case being left or right.

In two dimensions, a point (x,y) would be represented by a vector whose tail lies on the origin (0,0) and whose tip extends to the point (x,y). Note: x,y can be any point, even (0,0) itself, in which case the vector would have zero length.

    This special vector is called the "position vector." The two separate pieces of information we need in order to deduce the point which the vector is trying to represent is the length and direction. Length is also referred to as the magnitude of a vector, and in higher mathematics, the magnitude of a vector is called its "norm", and in particular, its "Euclidean Norm".  I will henceforth call the length of a vector its norm. The common notation for this is to put two bars around the vector: ||v||.

    In one dimension, the norm of a vector is identical to taking the modulus of the difference of the end value of x and the start value of x. In other words, if you want to find the norm of the vector in one dimensions, simply put the start point on zero, and take the modulus of the end point x. This is the actual value of the vector. In the case above, v=-2. The norm, or length of v is identical to the modulus to the vector, and the direction can be deduced by looking at its sign.

    In two dimensions, finding the norm is less intuitive: it is calculated by taking the positive square root of the sum of the squares of the x and y component of the vector, by the pythagorean theorem, and in three dimensions, the square root of the sum of the squares of the x, y and z components, and so on into n dimensions. In two dimensions, we give the direction of the vector by the angle it makes with the positive x-axis. In three dimensions, we need three separate angles, the angles it makes with each axis, and this carries on to n dimensions.

Now, there is one last thing I want to note: because the two key pieces of information embedded in the blue print of the vectors is length and direction, the starting points and end points do not matter. Hence, you can argue that the vector representing the point (2,3) could start arbitrarily any where. However, to make life easier, we tend to attach the tail of the position vectors to the origin, so the tip touches the point that we are interested in. Therefore, all points in our n-dimensional space can be uniquely represented by one and only one vector.
   As a quick review, there are two very important operations that can be done to vectors which I will assume that you are confident in. There is addition of vectors, which is visually found through the tip-to tail procedure, and the scalar multiplication of vectors: multiplying a vector by a number, called a "scalar," never affects its direction, but will multiply the norm by the scalar. Finally, we define a vector which is of length one along the x axis the i-hat unit vector, and a vector which is also of length one but point up the y-axis the j-hat unit vector. These vectors follow all the rules of addition and scalar multiplication just like any other vector.

    Let me illustrate first how to define a position vector for the point (2,3) on the xy plane. Consider two separate vectors, on which is pointing to the right and has 2 units of length, and the other pointing up and has 3 units of length. The vector pointing along the horizontal can be represented by a unit length vector i-hat, but scaled up by 2. Similarly, the vector pointing along the y-axis can be represented by a j-hat unit vector, but scaled up by a factor of 3. Again, where we place these vectors is arbitrary, so I will place them such that it will lie tip to tail. Ah! But that is vector addition, so really the position vector for (2,3) is identical to saying the sum of the horizontal and vertical vectors. Therefore, the position vector for (2,3) is

You will notice that there is an exact correspondence here: the position vector for a given (x,y) is simply the the x-value, a scalar, multiplied by the i-unit vector, and the y-value multiplied by the j-unit vector.  Therefore, for a position vector centred at the origin, the point (x,y) on the plane is represented by a vector r=xi+yj.
    We already established that for a given value of t (that lies in its domain) the parametric equations will output a coordinate ( x(t), y(t) ). For example, the point along the path at t=0 will be given by ( x(0), y(0) ). Now, the point on the curve at t=0 will be a point on the xy plane, and as I have shown earlier, this can be represented by a position vector r=x(0)i+y(0)j.
By that reasoning, we can define a separate position vector for t=1, which will then be r=x(1)i+y(1)j and t=2, which would be, you guessed it, r=x(2)i+y(2)j, and so on and all the infinite values of t in between, and for all the values of t for which this parametric curve is defined for.

    Now, you can immediately point out that if you give me an arbitrary value for t, I will give you a position vector. Well, that is suspiciously similar to the idea of a function, but with the only difference that the input is a scalar, a value for t, and the output is a vector. And that, ladies and gentleman, is an example of a vector-valued function, namely, a position vector valued function.

To represent the point (x(t),y(t)), we can define a position vector whose tail lies on the origin, and whose x and y components are given by the above formula.

Visualisation of a position vector function for any t in the closed interval [t0,t1].

  Vector Fields

Defining a position vector valued function turns out to be extremely useful for future use. In addition to this position vector valued function, other vector valued functions can be defined. For example, one could define a vector valued function in the xy plane which is not necessarily parameterised, but depends on x and y. In other words, instead of it being you give me a t and I give you a vector, we could also define a vector such that you give me a point on the plane or in space, and I give you a vector. Note, the vector is two dimensional, too. This vector is often visualised as being attached to the particular input point. This ends up being very very important by creating an infinite amount of vectors for each point on the plane, or in space, or in n dimensions, and can describe, for example, the force a particle would feel at that point. Whenever we have the same number of dimensions in the input and output, we can visualise the vector-valued function as a vector "field."
 In this case, as illustrated below, a point from a 2-dimensional input space gets mapped to a vector in the output space. As an example, observe how the point (2,3) gets mapped to the vector 2i+3j, according to the way I have defined the function.

The point (2,3) gets mapped onto the vector 2i+3j. The vector, by convention, not by fundamental mathematical laws, is centred at the origin.

Now, since the vector does not care where I place it along the xy plane, I can bring it from the origin and make the start point coincide with the point that I originally inputted into my function: (2,3). In a sense, I am merging the input and outputs spaces together, just like what you do when you graph regular single-variable scalar functions or even 2-variable scalar functions.

In just the same way I am perfectly allowed to chose to place my vector in the origin, I can place it starting from any point I want. In this case, so we can see 

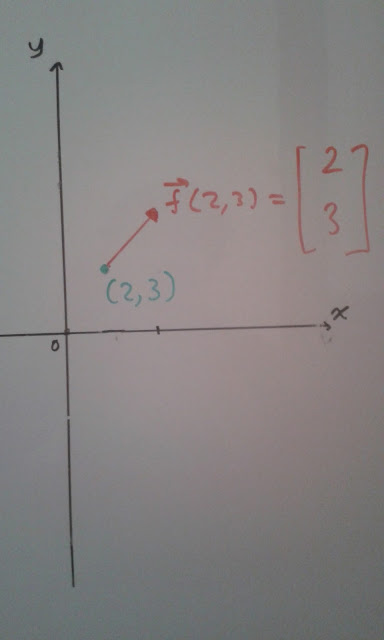Here, one can clearly see that the input, the green point, and the output, the red vector has been merged together onto a single xy plane.

 In theory, I can perform this to all the points on the xy plane and its output vectors, but it will take me quite a bit of time considering that there are an infinite amount of them! Therefore, I choose to display a subset of all the vectors that do exist. I used the website https://kevinmehall.net to graph the vector field in full f(x,y)=xi+yj. 

Vector fields then are super useful in physics as they can represent physical quantities. If you imagine fluid particle flowing through space, a vector associated to each point can very succinctly describe the velocity that a particular particle passing through that point would feel. Or, we can construct a vector field that would describe the force a positive test charge would feel at a given point in space due to another positive charge sitting at the origin of our coordinate system.

    And now we are developing ideas that will be exceptionally relevant and useful in our discussion of electricity and magnetism, particularly maxwell's equations. However, we shall now venture into the "calculus" of multivariable calculus. That shall be the topic of the next blog post.